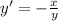Question

In(x^2+y^2) = e find derivative by using implicit differentiation

Answer 1

Given the equation:

`ln(x^2+y^2)=e`

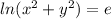
You can find its derivative by using Implicit Differentiation. In order to do this, you need to treat "y" as a function of "x".

The steps are:

1. Set up:

`\lbrack ln(x^2+y^2)\rbrack^(\prime)=(e)^(\prime)`

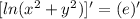
2. Apply the following Derivatives Rules:

`(d)/(dx)(lnu(x))=(1)/(u(x))\cdot u^(\prime)(x)`
`(d)/(dx)(k)=0`

Where "k" is a constant.

`(d)/(dx)(x^n)=nx^(n-1)`
`(d)/(dx)(ux^n)=nu(x)^(n-1)\cdot u^(\prime)(x)`

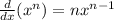
Then, you get:

`((1)/(x^2+y^2))(x^2+y^2)^(\prime)=0`
`((1)/(x^2+y^2))(2x+2y\cdot y^(\prime))=0`
`(2x+2yy^(\prime))/(x^2+y^2)=0`

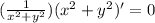
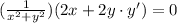
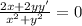
3. Solve for:

`y^(\prime)`

Then:

`2(x+yy^(\prime))=(x^2+y^2)(0)`
`y^(\prime)=(-2x)/(2y)`
`y^(\prime)=-(x)/(y)`

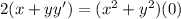
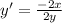
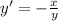
Hence, the answer is:

`y^(\prime)=-(x)/(y)`