Question

Which of the following is the correct vertex form of the quadraticf(x)=x²+2x-5?A) f(x)=(x+1)^2 -6B) f(x)=(x-1)^2 -6C) f(x)=(x-1)^2 +6D) f(x)=(x+1)^2 +6

Answer 1

We have that the vertex form of the quadratic function is:

`f(x)=a(x-h)^2+k`

where 'a' is a constant, and (h,k) is the point where the vertex of the parabola is.

In this case, we have the following function:

`f(x)=x^2+2x-5`

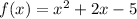
notice that if we move the -5 to the left side of the equation we have:

`f(x)+5=x^2+2x`

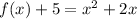
next, we can complete the square of x^2 + 2x. We can do this by dividing 2 by 2 and then elevating to the square the result, which is 1. Then if we add 1 on both sides of the equation we have:

`\begin{gathered} f(x)+5+1=x^2+2x+1 \\ \Rightarrow f(x)+6=(x+1)^2_{} \end{gathered}`

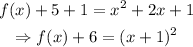
finally, we can move the 6 to the right side to get:

`\begin{gathered} f(x)+6=(x+1)^2 \\ \Rightarrow f(x)=(x+1)^2-6 \end{gathered}`

therefore, the correct vertex form of f(x) is f(x) = (x+1)^2 - 6