You need to remember the following properties for logarithms:
1. Quotient Property:
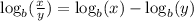
2. Power Property:
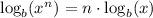
In this case, given the expression:
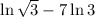
You need to remember the following property:
![\sqrt[n]{a^n}=a^{(n)/(n)}=a](https://img.qammunity.org/2023/formulas/mathematics/college/amz89dlryvzltfmeq7epy7niyz2nfr107m.png)
Then, you know that:
![\sqrt[]{3}=3^{(1)/(2)}](https://img.qammunity.org/2023/formulas/mathematics/college/lkoe0nsm2sveliucb0zewt4ekhde35oj9f.png)
Therefore, you can rewrite the expression as follows:
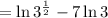
Now you can apply the Power Property:
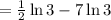
Notice that the logarithms have the same base and the same argument. Then, you can subtract them.
To make the procedure easier, you can subtract the fraction and the whole number first and then rewrite the result:
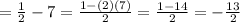
Therefore, rewriting the whole logarithmic expression, you get:
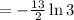
Hence, the answer is: Option B.