We need to find a function f(x) as shown below such that it models the oil spill covering,
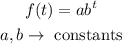
Therefore, in our case, since the oil spill initially covers 2mi^m,
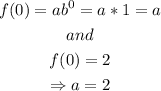
On the other hand, after 4 hours the area triples; therefore, at t=4, the covered area is 3*2=6mi^2. Use this fact to fnd bthe value of b, as shown below
![\begin{gathered} f(4)=2b^4 \\ and \\ f(4)=6 \\ \Rightarrow2b^4=6 \\ \Rightarrow b=\sqrt[4]{3}=(3)^{(1)/(4)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6aypt74zmuwsdddizmvo2az9q83vwlcmhs.png)
Thus, the exponential model is
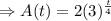
The answer is A(t)=2(3)^(t/4); A(t) is in i^2 ,and t is in hours.