Question

Let the universal Set,S have 118 elements. A and B are subsets of S. Set A contains 64 elements and Set B contain 26 elements. If the total number in either A or B is 79, How many elements are in A but not B ?

Answer 1

There are 53 elements in A but not in B

Step-by-step explanation

Given information

n(S) = 118

n(A) = 64

n(B) = 26

n(AUB) = 79

Step 1: We will need to find the elements that are both in set A and set B first using the below formula

`\text{ n\lparen A}\cup\text{ B\rparen = n\lparen A\rparen + n\lparen B\rparen - n\lparen A}\cap B)`

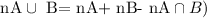
Step 2: Substitute the given into the formula in step 1

`\begin{gathered} \text{ 79 = 64 + 26 - n\lparen A}\cap B) \\ 79\text{ = 90 - n\lparen A}\cap B) \\ \text{ subtract 90 from both sides} \\ \text{ 79 - 90 = 90 - 90 - n\lparen A}\cap B) \\ \text{ - 11 = - n\lparen A}\cap B) \\ \text{ n\lparen A}\cap B)\text{ = 11} \end{gathered}`

Step 3: Find the element that is in A but not in B using the below number

`\begin{gathered} \text{ n\lparen A-}B)\text{ = n\lparen A\rparen - n\lparen A}\cap B) \\ \text{ n\lparen A - B\rparen = 64 - 11} \\ \text{ n\lparen A - B\rparen = 53} \end{gathered}`

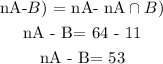
Hence, there are 53 elements in A but not in B