a) They ask to the cost function, and we know that there is a fixed cost of 18000 and that each canoe cost 20 to produce it, then we can write it mathematically as:
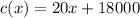
b) The revenue function is given by the selling price, which is 80, and the number of canoes sold, then we can write it mathematically as:

c) the break-even point is given when the revenues cover the costs, then is the intersection point of the two functions:
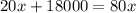
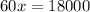

And we can replace it to find the other component:

So we can conclude that the break-even point is when is sold 300 canoes and the costs and the revenues are the same, that is $24000