The tree grew at a constant rate after being planted, i.e. it grew the same amount of feet each year.
Let "H" represent the height in feet and "p" the years after planting, you can represent the relationship between both variables as follows:
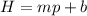
Where
m is the rate of change (slope) of the relationship
b is the height of the tree when it was planted (y-intercept)
Using the two ordered pairs of p and H, you can calculate the rate of change (m) of the relationship using the following formula:

Where
(p₁,H₁) represents one point of the relationship
(p₂,H₂) represents a second point of the relationship
You can use any two points shown on the table to determine the rate of change, I will use the points (10,25) and (7,19)
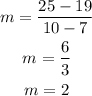
m=2 → this indicates that the tree grew 2ft/year.
The expression that shows this relationship can be written as:
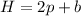
Now that we have determined the growth rate of the tree, we can calculate its starting height, just replace the expression with one ordered pair of time and height, for example, (3,11)
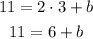
To calculate b, you have to subtract 6 to both sides of the equation

b=5 → indicates that the tree was 5ft tall when planted