Question

Find k so that the line containing the points (-5,k) and (4,6) is parallel to the line containing the points (7,4) and (3,-3) k=

Answer 1

For two lines to be parallel, the two lines must have the same slope. The slope of a line can be solved using the formula below:

`m=(y_2-y_1)/(x_2-x_1)`

For our first line, the points are (-5, k) and (4,6). The slope is:

`m=(6-k)/(4-(-5))=(6-k)/(9)`

For our second line, the points are (7, 4) and (3, -3). The slope is:

`m=(-3-4)/(3-7)=(-7)/(-4)=(7)/(4)`

Since the slope of the two lines must be the same for them to be parallel, we can say that:

`(6-k)/(9)=(7)/(4)`

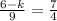
From the above equation, we can now solve for "k".

`\begin{gathered} (6-k)/(9)=(7)/(4) \\ 4(6-k)=7(9) \\ 24-4k=63 \\ 24-4k-24=63-24 \\ -4k=39 \\ (-4k)/(-4)=(39)/(-4) \\ k=-(39)/(4)or-9.75 \end{gathered}`

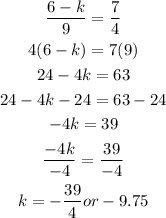
The value of k must be -39/4 or -9.75 for the two lines to be parallel.