To determine how much more than Ian will Lauren have in her account after the 20 years, you have to calculate how much interest they will acquire in the said time period.
Ian's account
This account compounds continuously, to calculate the accrued amount, you have to use the following formula:
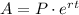
Where
A is the accrued amount
P is the principal amount
r is the interest rate expressed as a decimal value
t is the time periods, expressed in years
e is the natural number:
The principal amount is the initial investment P= $20000
The interest rate is 3%, to express it as a decimal value you have to divide it by 100:

The time period is t=20 years
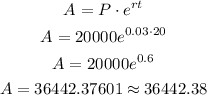
After 20 years, Ian will have $36442.38 in his account.
Lauren's account
This account compounds monthly, to determine the accrued amount after 20 years you have to apply the following formula:

Where
A is the accrued amount
P is the principal amount
r is the interest rate, expressed as a decimal value
n is the number of compounding periods per time unit, in this case the account compounds monthly, which means that there will be 12 compounding periods per year.
t is the time period.
The principal amount is the initial investment of $20000
The interest rate is 3%, to express it as a decimal value you have to divide it by 100:

The time period is also t=20 years, and the compounding periods is n=12
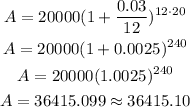
After 20 years, Lauren will have $36415.10
Finally, you have to calculate the difference between the accrued amount of Lauren's account and the accrued amount of Ian's account:
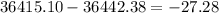
The difference is -27.28, which means that after 20 years Lauren will have $27.28 less than Ian.