Question

To estimate the length of a pond, a biologist walks 1,200 feet from point X to point Y, then turns 110 degrees and walks 1500 feet to point Z. What is the approximate length of the pond?

Answer 1

1568 ft

Step-by-step explanation:

By cosine law, we can calculate the length of XZ using the lengths of the other two sides of the triangle XY and YZ and the angle between them of 70 degrees.

Therefore, using cosine law, we can write the following equation

`\begin{gathered} (XZ)^2=(XY)^2+(YZ)^2-2(XY)(YZ)\cos70 \\ (XZ)^2=1200^2+1500^2-2(1200)(1500)\cos70 \end{gathered}`

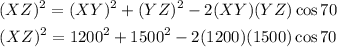
Solving for XZ, we get:

`\begin{gathered} (XZ)^2=2458727.48 \\ XZ=√(2458727.48) \\ XZ=1568.03\text{ ft} \end{gathered}`

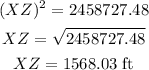
Therefore, the approximate length of the pond is 1568 ft