Answer;
A) 24 yards
B) (24 + 8√3)yards
C) 454.28 square yards
Explanations:
A) The triangle NPO is a right triangle. The length of the centre aisle NP is determined using the SOH CAH TOA identity;
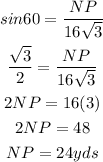
Hence the length of centre aisle is 24 yards
B) The measure of the base is LO
LO = LP + PO
Determine the length of LP and PO
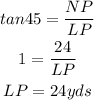

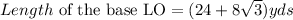
C) The area of the garden (triangle) is expressed as:
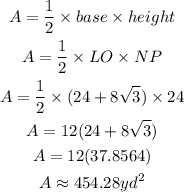
Hence the approximate area of the garden is 454.28 square yards