In this problem, we have a probability binomial distribution
we have that
in a department of 5 employees at most 2 are late
means
0 employees late and 5 employees not late
1 employee late and 4 employees not late
2 employees late and 3 employees not late
the formula to calculate the probability is equal to
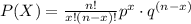
where
p=0.21
q=1-p=1-0.21=0.79
n=5
so
Step 1
Find out the probability when x=0 (0 employees late and 5 employees not late)
substitute given values
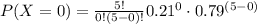
P(x=0)=0.3077
step 2
Find out the probability when x=1 (1 employee late and 4 employees not late)
substitute given values
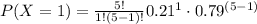
P(x=1)=0.4090
step 3
Find out the probability when x=2 (2 employees late and 3 employees not late)
substitute
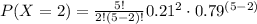
P(x=2)=0.2174
therefore
the probability on a given day that in a department of 5 employees at most 2 are
late is equal to
P(x≤2)=P(x=0)+P(x=1)+P(x=2)
P(x≤2)=0.3077+0.4090+0.2174
P(x≤2)=0.9341
the answer is
P=0.9341