Given:
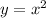
Let's graph the parabola.
To graph the parabola, apply the vertex form of a parabola:
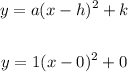
Thus, we have the values:
a = 1
h = 0
k = 0.
• The vertex is:
(h, k) ==> (0, 0)
• The parabola opens up since the value of ,a ,is positive.
Now, let's find more points using the equation.
• When x = 1
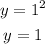
When x = -1:
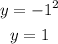
When x = 2:
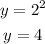
When x = -2:
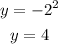
When x = 3:
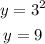
When x = -3:
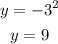
Therefore, we have the points:
(0, 0), (1, 1), (-1, 1), (2, 4), (-2, 4), (3, 9), (-3, 9)
Plot the points and connect them to form a parabola.
We have the graph below: