Question

Drag the tiles to the correct boxes to complete the pairs. Not all tiles will be used.Consider the function,f(1) = 21 - 6Match each transformation of Rx) with its description.g() = 21 – 109(0) = 21 - 14g(1) = 81 - 4g(t) = 21 - 2g(1) = 81 - 24g(I) = 85 - 6shifts 1x) 4 units rightstretches x) by a factorof 4 away from the x-axiscompresses (x) by a factorof 4 toward the y-axisshifts x 4 units down

Answer 1

The function f(x) is:

`f(x)=2x-6`

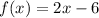
We have to find the functions that perform the following transformations:

a) Stretches f(x) by a factor of 4 away from the x-axis.

This is a vertical stretching, meaning that the values of y=f(x) are scaled by the factor.

This can be represented as:

`g(x)=4\cdot f(x)=4(2x-6)=8x-24`

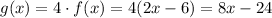
Answer: g(x) = 8x - 24

b) Shifts f(x) 4 units right

This is a translation in the x-axis, in the direction of the positive values.

Then:

`g(x)=f(x-4)=2(x-4)-6=2x-8-6=2x-14`

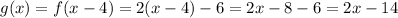
Answer: g(x) = 2x - 14

c) Compresses f(x) by a factor of 1/4 towards the y-acis.

In this case is an horizontal stretching, and the input x is divided by the factor of compression.

Then:

`g(x)=f((x)/((1)/(4)))=f(4x)=2(4x)-6=8x-6`

Answer: g(x) = 8x - 6

d) Shifts f(x) 4 units down.

This is a vertical translation and can be written as:

`g(x)=f(x)-4=(2x-6)-4=2x-10`

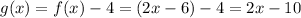
Answer: g(x) = 2x - 10