Question

GEOMETRY Express the volume of each solid as a monomial. a. m3n3b. m3n4c. m4n4d. m4n5

Answer 1

Consider the image given below

The image above is a cuboid and the volume of a cuboid is given by the formula

`\text{Volume of cuboid= L x W x H}`

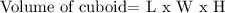
Where

`\begin{gathered} L=length=m^3n \\ W=\text{width}=mn^3 \\ H=\text{height}=n \end{gathered}`

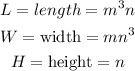
Substituting into the formula, we have

`\text{Volume of cuboid=m}^3n* mn^3* n`

Simplifying the expression we have

`m^3* m^1* n^1* n^3* n^1`

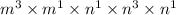
Applying the rule of indices i.e when the base are the same, we add their powers

Hence.

`\begin{gathered} m^(3+1)* n^(1+3+1) \\ m^4* n^5 \end{gathered}`

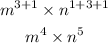
Therefore, the monomial becomes

`m^4n^5`

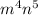
Answer ; Option D