Question

A function, h(x), is defined as shown.1/x-4₁ x ≤0h(x) = x - 3,0 < x < 3-x-2,-2, x ≥ 4Which graph represents h(x)?Ih(x)54+3+24--4-3-2-1₁--2+-31 23442+--4-3-2-₁--2--3417h(x)23↓85MOB32+3-2-1₁.-2<-3h(x)234

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given piecewise function

STEP 2: Get the graph of the function

The graph above shows the function at every points of x indicated in the question. The red line is for the first function which is:

`(1)/(4)x-4\lbrace x\leq0\rbrace`

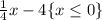
The blue line shows the function

`(1)/(3)x-3\lbrace0<strong>The green line shows the function:</strong>[tex](1)/(2)x-2\text{ }\lbrace x\ge4\rbrace`

Therefore, the correct graph from the options will be the one that has an equivalent plot combined and will be: