SOLUTION
Now, on a die of 6 faces, we have 3 even numbers which are 2, 4 and 6
Probability is calculated as
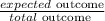
So, number of even number is 3, total die faces is 6
Probability of getting an even number becomes

Also there is only 1 face with 1.
So probability of getting a 1 is

Now, probability of getting an even number or a 1, means we add both, we have
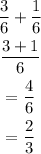
hence the answer is 2/3, the last option nswe