Question

In 5 hours, an experienced cook prepares enough lies to supply a local restaurant’s daily order. Another cook prepares the same number of pies in 6 hours. Together with a third cook they prepare the pies in 2 hours find how long it takes the third cook to prepare the pies alone The third cook prepares the pies alone in ? hours

Answer 1

Given:

Number of hours it takes the first cook = 5 hours

Number of hours it takes the second cook = 6 hours

Together with a thrid cook, the number of hours it takes 2 hours.

Let's find the time it will take the third cook to prepare the pie alone.

Let x represent the number of hours it takes the third cook to prepare alone.

Let y represent the number of pies.

We have the following:

• Number of pies the first cook prepares in 1 hour:

`(y)/(5)`

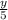
• Number of pies the second cook prepares in 1 hour:

`(y)/(6)`

• Number of pies the third cook to prepare in one hour:

`(y)/(x)`

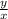
Number of pies the three cooks prepare altogether in one hour:

`(y)/(2)`

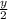
Thus, we have the equation:

`(y)/(5)+(y)/(6)+(y)/(x)=(y)/(2)`

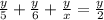
Let's solve for y in the equation above.

Facor out y from the left side

`y((1)/(5)+(1)/(6)+(1)/(x))=(y)/(2)`

Divide both sides by y:

`\begin{gathered} (y((1)/(5)+(1)/(6)+(1)/(x)))/(y)=((y)/(2))/(y) \\ \\ (1)/(5)+(1)/(6)+(1)/(x)=(1)/(2) \end{gathered}`

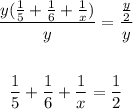
Combine like terms:

`\begin{gathered} (1)/(5)+(1)/(6)+(1)/(x)=(1)/(2) \\ \\ (6+5)/(30)+(1)/(x)=(1)/(2) \\ \\ (11)/(30)+(1)/(x)=(1)/(2) \end{gathered}`

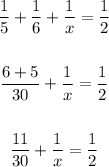
Subtract 11/30 from both sides:

`\begin{gathered} (11)/(30)-(11)/(30)+(1)/(x)=(1)/(2)-(11)/(30) \\ \\ (1)/(x)=(1)/(2)-(11)/(30) \\ \\ (1)/(x)=(15-11)/(30) \\ \\ (1)/(x)=(4)/(30) \end{gathered}`

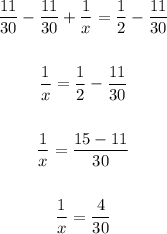
Solving further:

`\begin{gathered} (x)/(1)=(30)/(4) \\ \\ x=7.5 \end{gathered}`

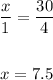
Therefore, the third cook prepares the pies alone in 7.5 hours.

ANSWER:

7.5 hours