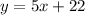Question

Which equation could be a prediction equation for this set of data

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Draw the given plot

The prediction equation can be determined by finding the equation of the line.

STEP 2: Write the standard slope-intercept form of the equation of a line

`\begin{gathered} y=mx+c \\ where\text{ m is the slope and c is the y-intercept} \end{gathered}`

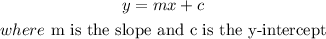
STEP 3: Find the slope

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ From\text{ the image in step 1,} \\ (x_1_,y_1)=(36,200) \\ (x_2,y_2)=(16,100) \\ \\ \therefore m=(100-200)/(16-36)=(-100)/(-20)=5 \end{gathered}`

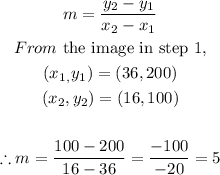
STEP 4: Find the equation of the line using the formula below

`\begin{gathered} y-y_1=m(x-x_1) \\ \text{Using \lparen}36,200) \\ y-200=5(x-36) \\ y-200=5x-180 \\ y=5x-180+200 \\ y=5x+20 \end{gathered}`

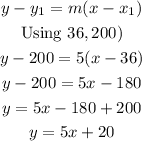
Since it is a predictive equation, the equation that is approximately close to the equation can be seen in the options.

Hence, the predictive equation is:

`y=5x+22`