Given:
A 9000 deposit accumulates to 9883, compounded annually for 8 years.
So, P = 9000, A = 9883, t = 8 years, n = 1
We will find the interest rate = r
We will use the following formula:

Substitute the given values:
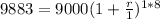
Solve the equation to find (r):
![\begin{gathered} (1+r)^8=(9883)/(9000) \\ \\ 8*ln(1+r)=ln((9883)/(9000))\approx0.09359 \\ \\ ln(1+r)=(0.09359)/(8)\approx0.0116989 \\ \\ 1+r=e^^(0.0116989)\approx1.011767 \\ \\ r=1.0117676-1=0.0117676 \\ \\ r=1.17676\% \end{gathered}]()
So, the answer will be:
The interest rate is 1.17676%