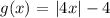The graph is a plot of an absolute value function.
The general equation of an absolute value function is expressed as
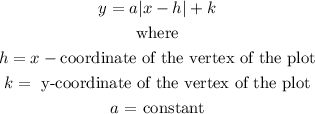
Thus, given the graph below
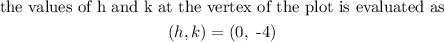
Thus,
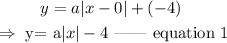
From the graph, taking either zeros of the function (that is, x = -4 or x = 4)
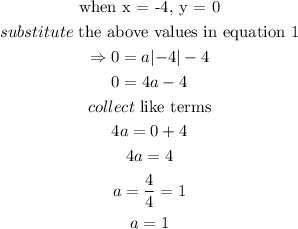
Thus, the equation of the plot is given as
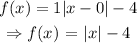
To solve for g(x):
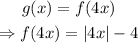
Thus,