Question

Someone helped me with this but I was taught to subtract the 6 feet from the 12. any clarification.

Answer 1

Let's draw the scenario to better understand the problem:

Let's focus on the triangle formed by the scenario:

A.) Let's determine the distance of his eyes from the birdhouse, it is represented by x.

Since the triangle formed is a right triangle, we can determine the value of x using the Pythagorean Theorem.

`\text{ c}^2=a^2+b^2`

We get,

`\text{ c}^2=a^2+b^2`
`\text{ (x)}^2=(6)^2+(15)^2`
`\text{ x}^2=36^{}+225`
`\text{ x}^2=261`
`\text{ }\sqrt{\text{x}^2}=√(261)`
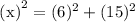
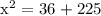
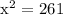
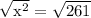
`\text{x }=3\sqrt[]{29}\text{ = 16.1554944214 }\approx\text{ 16.16 Ft.}`

Therefore, the distance of his eyes is 16.16 Ft. away from the birdhouse.

B.) Let's determine the angle of elevation for him to look up at the birdhouse.

We will be using the Tangent Function.

`\text{ Tangent }\theta\text{ = }(a)/(b)`
`\text{ Tangent }\theta\text{ = }(6)/(15)`
`\text{ }\theta=Tangent^(-1)((6)/(15))`
`\text{ }\theta=21.80140948635\text{ }\approx21.80^(\circ)`

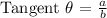
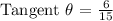
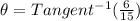
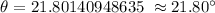
Therefore, the angle of elevation for him to look up at the birdhouse is 21.80°