Question

This is question 10 from p. 495 of the book.) Show all five steps for this hypothesis testing problem. Be sure to give me the null and alternative hypotheses, the test value (z), the p-value, and the conclusion. You can either type your work here, or write it out on paper and submit a scan/picture of your work.A real estate agent compares the selling prices of randomly selected homes in two municipalities in southwestern Pennsylvania to see if there is a difference. The results of the study are shown. Is there enough evidence to reject the claim that the average cost of a home in both locations is the same? Use α = 0.01.

Answer 1

Given data:

Scott

`\begin{gathered} Sample\text{ mean (}\mu_1)=\text{ \$93,430} \\ S.d\text{ (}\sigma_1)=\text{ \$5602} \\ Sample-size(n_1\text{) = 35} \end{gathered}`

Ligonier

`\begin{gathered} Sample\text{ mean (}\mu_2)=\text{ \$98,}043 \\ S.d\text{ (}\sigma_2)=\text{ \$4731} \\ Sample-size(n_2\text{) = 4}0 \end{gathered}`

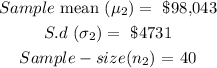
step 1: State the null hypothesis (H₀) and alternative hypothesis (H1)

`\begin{gathered} H_0=\mu_1-\mu_2=0 \\ H_1=\mu_1-\mu_2\\e0 \end{gathered}`

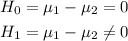
step 2: Find the critical value with a significance σ= 0.01

The critical value- two-tailed is: -2.576 and 2.576

Note that,

`If,z>2.576\text{ or }z<-2.576\text{ },\text{ reject the null hypothesis}`

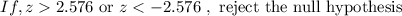
step 3:

Find the z-score

`\begin{gathered} z=\frac{(X_1-X_2)-(\mu_1-\mu_2)}{\sqrt{(\sigma^2_1)/(n_1)+(\sigma^2_1)/(n_1)}} \\ z=\frac{(93,430-98,043)-0}{\sqrt[]{(5602)/(35)^2+(4731)/(40)^2_{}}} \\ z=(-4613)/(1206.73) \\ z=-3.823 \end{gathered}`

step 4: Since, z= -3.823 < -2.576 (critical value)

Therefore, we reject the null hypothesis - we can conclude that there is enough evidence to reject the claim that the average cost of a home in both locations is the same.

There is a significant difference in house prices.