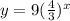Question

Write an exponential function for a graph that includes the points (1, 12) and (0,9).

Answer 1

The exponential function is;

`y=9((4)/(3))^x`

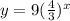
Step-by-step explanation:

Given that the function is an exponetial function.

It is of the form;

`y=ab^x`

And the function contains the points;

`\begin{gathered} (1,12) \\ \text{and} \\ (0,9) \end{gathered}`

so, substituting the values of x and y for each point;

`\begin{gathered} 12=ab^1 \\ 12=ab\text{ -------1} \\ 9=ab^0 \\ 9=a\text{ ----------2} \end{gathered}`

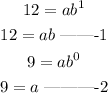
dividing equation 1 by 2;

`\begin{gathered} (12)/(9)=(ab)/(a) \\ b=(12)/(9) \\ b=(4)/(3) \\ \text{and } \\ a=9 \end{gathered}`

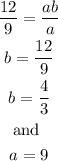
Therefore, substituting a and b, the equation gives;

`\begin{gathered} y=ab^x \\ y=9((4)/(3))^x \end{gathered}`

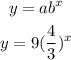
Therefore, the exponential function is;

`y=9((4)/(3))^x`