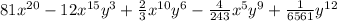We need to expand the following binomial:
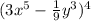
using binomial theorem. This theorem states that:
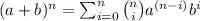
where
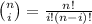
In this problem, we have:
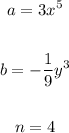
Part (a)
To express the expansion, we use the following sum in summation notation:
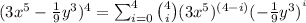
This can also be written as:
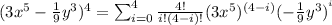
Part (b)
Simplifying the terms, we obtain:
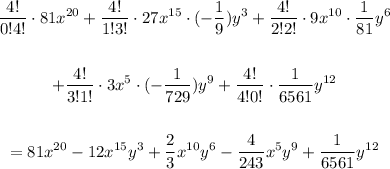
Therefore, the simplified terms of the expansion are: