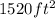To solve this problem and determine how many square feet of fence would be required, we have to find the surface area of the figure.
Step 1. Find the area of one of the rectangles:
To find this red area, multiply the base times the height of the rectangle:

Step 2. Since the figure has 4 rectangles that are equal, multiply the previous are by 4:
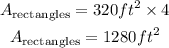
Step 3. Find the area of one of the triangles:
To find this area, we use the formula:
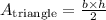
Where b is the base, in this case, 10 ft, and h is the height of the triangle, in this case, 12 ft:
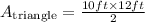
Solving the operations:
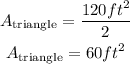
Step 4. As we did with the area of the rectangle, in this case for the triangle, we also have to multiply it by 4 since there are 4 triangles:
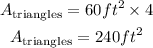
Step 5. The last step is to add the area of the rectangles and the area of the triangles to find the total surface area:
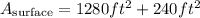
The result is:
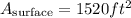
Answer: