Apply z-score
Given data
![\begin{gathered} \operatorname{mean}\text{ }\mu\text{ = 100.5} \\ \text{Standard deviation }\sigma\text{ = 1.5} \\ x\text{ = 102.1} \end{gathered}]()
Here, we use the normal distribution formula below to calculate the answer.
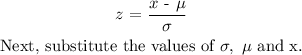
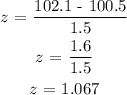
Next, use the normal distribution table to find probability.
From the normal distribution table,
The probability that the mean content is less than 102.1 mL = 0.3554
Final answer = 0.3554