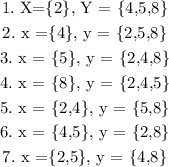This is an exercise of operation between sets. This is the data we know:
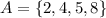
Part a)
B = {4}
We must find a subset C such that B ∩ C = 0, and B ∪ C = A. In other words, we can say that C = A - B. Using Venn diagrams we see that C = {2,5,8}:
(Here is an image of the exercise)
Part b)
D = {2,8}
We must find a subset E such that D ∩ E = 0, and D ∪ E = A. In other words, we can say that E = D - A. Using Venn diagrams we see that E = {4,5}
Here is an image:
Part c)
X and Y are said to be distintic pairs of disjoint non-empty subsets of the set A if the followings are true:
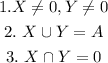
In this case, there are 7 distintic pairs of disjoint non-empty subsets of the set A and they are: