Answer:
Given that,
One integer is 4 more than another.
Their product is 165.
Let the intergers be x and y.
Let x be the larger integer.
we get,


Substitute equation (1) in equation (2), we get,
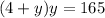
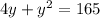
Solving this we get,

we get,
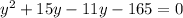
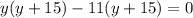
Taking y+15 as common, we get
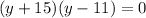
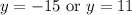
Hence there are two possible solutions
when y=-15, we get x=-11,
And when y=11, we get x=15
Largest integer = -11 or 15
Smallest integer = -15 or 11
Answer is:
Largest integer = -11 or 15
Smallest integer = -15 or 11