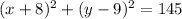Solution
- The general equation of a circle is given by:

- Since the center of the circle is at (-8, 9), then it implies that
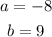
- Thus, we can write the equation as follows
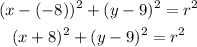
- As it is, the equation is still incomplete because we don't have the radius (r).
- This radius can be gotten by applying the condition given in the question that "The circle passes through the origin" .
- This means that the circle, when drawn, passes through the point (0, 0).
- Thus, we can substitute x = 0 and y = 0 into our incomplete equation and find the value of r.
- This is done below:
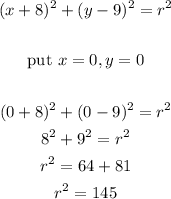
- Thus, the equation of the circle with center (-8, 9) is:
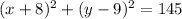
Final Answer
The answer is