Solution
- Let the amount invested in stocks, bonds, and CDs be s, b, and c.
- The total fund is 195000. This means:
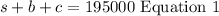
- We are also told that the interests from the investments are
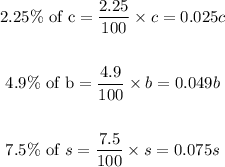
- We are told that the income from the investments is $10972.50. This implies that:
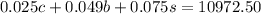
- Lastly, we are also told that $65000 was invested more in bonds than CDs. This implies that:
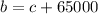
- Thus, we have 3 simultaneous equations that we can solve.
- The solution steps for solving the equations are given below:
![\begin{gathered} b=c+65000 \\ \text{ Substitute this expression for b into the other two equations,} \\ \\ 0.025c+0.049b+0.075s=10,972.50 \\ 0.025c+0.049(c+65000)+0.075s=10972.50 \\ \text{ Simplifying, we have:} \\ 0.074c+3185+0.075s=10972.50 \\ \text{ Subtract 3185 from both sides} \\ 0.074c+0.075s=10972.50-3185 \\ \\ \therefore0.074c+0.075s=7787.50\text{ \lparen Equation 4\rparen} \\ \\ s+b+c=195,000 \\ s+c+65000+c=195,000 \\ s+2c=195000-65000 \\ s+2c=130000\text{ \lparen Equation 5\rparen} \\ \\ \text{ From Equation 5, we have:} \\ s=130000-2c \\ \text{ Substitute the expression of s into Equation 4} \\ 0.074c+0.075(130000-2c)=7787.50 \\ 0.074c+9750-0.15c=7787.50 \\ -0.076c=7787.50-9750 \\ -0.076c=-1962.50 \\ \text{ Divide both sides by -0.076} \\ \\ (-0.076c)/(-0.076)=(-1962.50)/(-0.076) \\ \\ c=\$25,822.37 \\ \\ \text{ Thus,} \\ s=130000-2c \\ s=130000-2(25,822.37) \\ s=\$78,355.26 \\ \\ b=c+65,000 \\ b=25,822.37+65,000 \\ b=90,822.37 \end{gathered}]()
Final Answer
The amounts invested are:
Bonds: $90,822.37
Stocks: $78,355.26
CDs: $25,822.37