Given the area of the rectangle, WXYZ = 115.5 square inches
As shown in the figure: PQ = 4 in
so, the length of WX = 2 PQ = 2 x 4 = 8 in
The area of the rectangle =
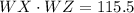
So,
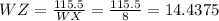
The length of XZ will be calculated using the Pythagorean theorem:
![\begin{gathered} XZ^2=WX^2+WZ^2=8^2+14.4375^2=272.44 \\ \\ XZ=\sqrt[]{272.44}=16.5058 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/tunwg67cdxvc9e4uazwx5yw2e0o6jvyzr9.png)
to the nearest tenth XZ = 16.5 inches
The perimeter of the triangle XYZ = XY + YZ + XZ
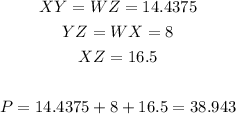
Rounding to the nearest tenth
so, the answer will be:
The perimeter of the triangle XYZ = 38.9 inches