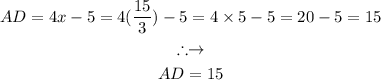Question

What is the value of side AD in picture below

Answer 1

`AD=15`

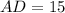
Step-by-step explanation: We know that in any given parallelogram the opposite sides are equal, therefore for the given parallelogram we can say the following:

`DC=AB`

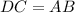
From this we can form the following equation for the sides:

`DC=AB\rightarrow3x+5=6x-10\rightarrow(1)`

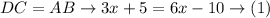
Solving (1) for x gives:

`\begin{gathered} 3x+5=6x-10\rightarrow3x+5+10=6x \\ \therefore\rightarrow \\ 3x+15=6x\rightarrow15=6x-3x=3x\rightarrow3x=15 \\ \therefore\rightarrow \\ x=(15)/(3) \\ x=5 \end{gathered}`

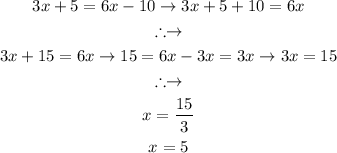
Therefore the value of the AD side is:

`\begin{gathered} AD=4x-5=4((15)/(3))-5=4*5-5=20-5=15 \\ \therefore\rightarrow \\ AD=15 \end{gathered}`