1 Answer

Haferblues · Answer 1 · 2023-09-17T09:30:42+0000

a. The given equation is:

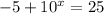
The first step is adding 5 to both sides:

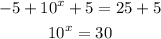
$\begin{gathered} -5+10^x+5=25+5 \\ 10^x=30 \end{gathered}$

The next step is to apply logarithm to both sides (Kim didn't do it and it is a mistake):

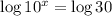
$\log 10^x=\log 30$

Apply the properties of logarithms:

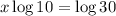
$x\log 10=\log 30$

Divide both sides by log 10 and solve for x:

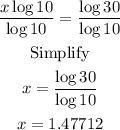
$\begin{gathered} (x\log10)/(\log10)=(\log 30)/(\log 10) \\ \text{Simplify} \\ x=(\log30)/(\log10) \\ x=1.47712 \end{gathered}$

The mistake that Kim made was not using the logarithm in the second step.

b. Solve for x:

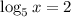
$\log _5x=2$

We can relate logarithms to exponential function as follows:

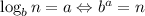
$\log _bn=a\Leftrightarrow b^a=n$

Then, we can say that:

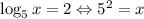
$\log _5x=2\Leftrightarrow5^2=x$

Kim applied the wrong formula and made a^b=n, that was the mistake.

And now we can solve for x:

$\begin{gathered} x=5^2 \\ x=5\cdot5 \\ x=25 \end{gathered}$

Please log in or register to add a comment.