Step-by-step explanation
In this problem, we have the inequality:
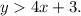
Graph
To plot the inequality, we paint all the points that lie in the region strictly over the line y = 4x + 3:
Part a
To find two points associated with the line, we replace the values x = 0 and x = 1 in the equation:
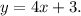
We get the points:

Part b
From the graph above, we see that the point (0, 6) is in the region that satisfies the inequality.
Replacing the coordinates of the point in the inequality, we see that:
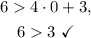
Answer
Part a
• The point ,(0, 3), is on the line y = 4x + 3.
,
• The point ,(1, 7), is on the line y = 4x + 3.
Part b
• The point ,(0, 6), satisfies y > 4x + 3.