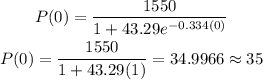Given the logistic growth model
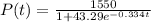
we want to find the initial amount of bacteria in this problem. If we are talking about the initial amount, we have t = 0 since time doesn't lapse yet for the growth of the bacteria. Hence, for t = 0, the amount of bacteria will be