Question

Are the following equations parallel, perpendicular or neither?y = -1/2x + 310x - 5y = 15A. ParallelB. PerpendicularC. Neither

Answer 1

By definition you know that the parallel lines have the same slope and that the slopes of the perpendicular lines satisfy the equation

`\begin{gathered} m_2=(-1)/(m_1) \\ \text{ Where }m_1\text{ and }m_2\text{ are the slopes of lines 1 and 2, respectively} \end{gathered}`

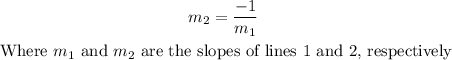
So, you can take the equation of the second line to the form

`\begin{gathered} y=mx+b \\ \text{ Where} \\ m\text{ is slope of the line} \\ b\text{ is y-intercept} \end{gathered}`

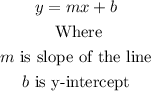
Then you have

`\begin{gathered} 10x-5y=15 \\ \text{ Subtract 10x from both sides of the equation} \\ 10x-5y-10x=15-10x \\ -5y=15-10x \\ \text{ Divide by -5 on both sides of the equation} \\ (-5y)/(-5)=(15)/(-5)-(10x)/(-5) \\ y=-3+2x \\ y=2x-3 \end{gathered}`

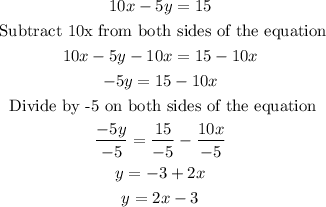
Now you know that the slope of the first line is -1/2 and the slope of the second line is 2, that is

`\begin{gathered} m_1=-(1)/(2) \\ m_2=2 \end{gathered}`

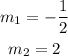
Let is see if the lines are perpendicular

`\begin{gathered} m_2=(-1)/(m_1) \\ 2=((-1)/(1))/((-1)/(2)) \\ 2=(-1\cdot2)/(1\cdot-1) \\ 2=(2)/(1) \\ 2=2 \end{gathered}`

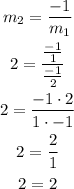
Since we arrive at a true statement, then the lines are perpendicular.

Therefore, the correct answer is B. Perpendicular.