Question

A private jet can fly 942 miles against a 18-mph headwind in the same amount of time it can fly 1158 miles with a 18-mph tailwind. Find the speed of the jet.

Answer 1

The speed of the jet is 175 mph

Explanation:

Let x be the speed of the jet.

The speed of the wind is 18 mph.

If the jet can fly 942 miles against the headwind:

`x=(942)/(t)+18\text{ \lparen1\rparen}`

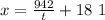
If it can fly 1158 nukes with an 18 mph tailwind, therefore:

`x=(1158)/(t)-18\text{ \lparen2\rparen}`

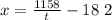
Equalize, and solve for t using equations (1) and (2).

`\begin{gathered} (942)/(t)+18=(1158)/(t)-18 \\ (942)/(t)-(1158)/(t)=-18-18 \\ -(216)/(t)=-36 \\ t=(-216)/(-36) \\ t=6\text{ hours} \end{gathered}`

Now, knowing the time substitute it into the equation and solve for the speed of the jet.

`\begin{gathered} x=(1158)/(t)-18 \\ x=175\text{ mph} \end{gathered}`

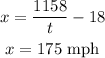
The speed of the jet is 175 mph.