We will use a simultaneous approach since the rates are seemingly different.
We will create a relationship using the general line equation, y = mx + c.
Where:
y = Cost, C according to our question
m = line gradient
x = no of shirts, n
c = line intercept on y / cost axis, we will call this b since we already have C
Thus, we will have:

So, inputting variables from our question, we have:

We now substitute this value of m into the equation 1 to get:
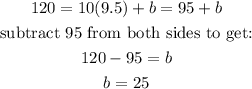
Finally, we substitute the values of m and b into equation 0 to get:
C = 9.5n + 25