Given the points
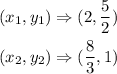
To find the distance, d, between the two points,
The formula is
![d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/be685jmxw05hm2tq94m5iuge2xjynn1hfn.png)
Substitute the values into the formula of the distance between two points above
![\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ d=\sqrt[]{((8)/(3)-2)^2+(1-(5)/(2))^2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/uy2a3c501k1zj3eqe16yq3csf9dpfug0jr.png)
Solve to find d,
![\begin{gathered} d=\sqrt[]{((8)/(3)-2)^2+(1-(5)/(2))^2} \\ d=\sqrt[]{((2)/(3))^2+(-(3)/(2))^2} \\ d=\sqrt[]{(4)/(9)+(9)/(4)} \\ d=\sqrt[]{(97)/(36)}=\frac{\sqrt[]{97}}{6} \\ d=\frac{\sqrt[]{97}}{6}=1.64\text{ (two decimal places)} \\ d=1.64\text{ (two decimal places)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/u5rjoz8r06elk5h7op8l10ak6wclgd4ssk.png)
Hence, the simplest radical form of the distance, d, between the two given points is 1.64 ( two decimal places).