We are given a normal distribution with a mean of 8 and a standard deviation of 0.6. Since the probability is normally distributed we need first to find the z-score of the distribution, to do that we use the following formula:
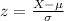
We have the following values:
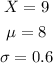
Replacing the values we get:
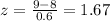
Now we use a normal distribution table to determine the probability for this z-score. That probability is:
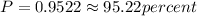
Therefore, the probability is 95.22 %