Question

To solve a system of inequalities so you can graph it how do you change these two equations into something like the two that are on number one?Problem #2.

Answer 1

Step-by-step explanation

Problem #2

We must find the solution to the following system of inequalities:

`\begin{gathered} 3x-2y\leq4, \\ x+3y\leq6. \end{gathered}`

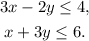
(1) We solve for y the first inequality:

`-2y\leq4-3x.`

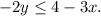
Now, we multiply both sides of the inequality by (-1), this changes the signs on both sides and inverts the inequality symbol:

`\begin{gathered} 2y\ge-4+3x, \\ y\ge(3)/(2)x-2. \end{gathered}`

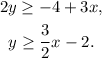
The solution to this inequality is the set of all the points (x, y) over the line:

`y=(3)/(2)x-2.`

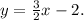
This line has:

• slope m = 3/2,

,

• y-intercept b = -2.

(2) We solve for y the second inequality:

`\begin{gathered} x+3y\leq6, \\ 3y\leq6-x, \\ y\leq-(1)/(3)x+2. \end{gathered}`

The solution to this inequality is the set of all the points (x, y) below the line:

`y=-(1)/(3)x+2.`

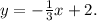
This line has:

• slope m = -1/3,

,

• y-intercept b = 2.

(3) Plotting the lines of points (1) and (2), and painting the region:

• over the line from point (1),

,

• and below the line from point (2),

we get the following graph:

Answer

The points that satisfy both inequalities are given by the intersection of the blue and red regions: