To solve the equation we must change cos(8x) to cos(4x) using the expression of double angles
cos(8x) = 2cos^2(4x) - 1
2cos^2(4x) - 1 + cos(4x) = 0
Arrange the terms
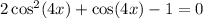
Now let us factorize it into two brackets
(2cos(4x) - 1)(cos(4x) + 1) = 0
Now equate each bracket by 0
cos(4x) + 1 = 0
cos(4x) = -1
The value of cos = -1, when 4x = pi
You must find the domain of 4x
The domain of x is [0, 2pi]
The domain 4x is [0, 8pi]
So you have 4 cycles of the angle
So you must add 2pi for the angle in each cycle then divide the angle by 4
4x = pi, 4x = 3pi , 4x = 5pi, 4x = 7pi
Divide all by 4
x = pi/4, 3pi/4, 5pi/4, 7pi/4
Now let us do the same with the 2nd bracket
2cos(4x) - 1 = 0
2cos(4x) = 1
cos(4x) = 0.5
Cos is positive in 1st and 4th quadrants
The angle which has cos = 0.5 is pi/3
So 4x = pi/3 or 2pi - pi/3 = 5pi/3
Add for each one 2pi as we did with the first value 4 times
4x = pi/3, pi/3 + 2pi, pi/3 + 4pi, pi/3 + 6pi,
4x = pi/3, 7pi/3, 13pi/3, 19pi/3
Divide all by 4
x = pi/12, 7pi/12, 13pi/12, 19pi/12
The solution for 5pi/3
4x = 5pi/3, 5pi/3 + 2pi, 5pi/3 + 4pi, 5pi/3 + 6pi
4x = 5pi/3, 11pi/3, 17pi/3, 23pi/3
Divide all by 4
x = 5pi/12, 11pi/12, 17pi/12, 23pi/12
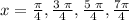
This answer for the first bracket
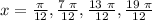
This answer for the 1st angle in the 2nd bracket
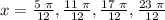
This answer for the second angle in the 2nd bracket