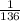Find the probability that the first winner randomly selects the card for the pizza topped with red peppers and green olives.
We must first find all the possibilities for the two topping pizzas ( 2 distinct toppings) that corresponds to the number if cards.
When choosing any topping we have 17 options and after that for the second topping we have 16 options

Here we repeat each option twice because it appears for example (green peppers, onions) and (onions,green peppers) , to eliminate the ones that we repeat, we divide by 2.
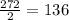
This corresponds to the combination of 17 combined by 2, 136 possibilities.
Then, the probability that the first winner randomly selects the card for the pizza topped with red peppers and green olives is: