Question

You want to take a hot bath in your mountain cabin. Your bathtub holds 200L of water. The stream outside is your only source of water and it is cold (6 °C). You need to heat your bathwater to 40 °C. Your only source of fuel is beetle-killed wood (which has a heat content of 18kJ/g. a) How much heat energy is required to heat the water in your bathtub?b)How many kg of wood would you need to burn 100% efficiency to heat your tub?c)Assuming you are only 30% efficient in heating your water with the wood fire, how many kg of wood would you need to burn to heat your bathtub?

Answer 1

The question gives information on volume and temperature of a tub full of water (Volume = 200 L and Temperature = 6°C) and asks us to calculate how much energy would be necessary to heat the water up to 40°C.

a) To calculate the amount of heat energy needed to heat the water from 6°C to 40°C, we can use the following formula:

`Q=m* c*\Delta T`

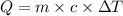
where Q is the amount of heat energy, m will be the mass of water, c is the specific heat of water (I'll be using c = 4200 J/kg°C) and AT is the variation of temperature.

The first step is to define the mass of water that should be heated. Since we have the information that the bath tub holds 200 L of water and water density is approximately 1 kg/L, we can use mass = 200 kg of water.

Next, we can calculate the amount of heat energy:

Therefore, 2.856 x 10^4 kJ are needed to heat the water in the bathtub.

b) Now, we need to calculate how much beetle-killed wood (which has a heat content of 18kJ/g) we would need to use to heat the water in the bathtub, considering 100% efficiency.

From the last item, we know the amount of energy needed to heat the bathtub (2.856 x 10^4 kJ) and we can relate it to the energy released by 1 g of wood:

18 kJ --------------- 1 g of wood

28560 kJ --------- x

Solving for x, we have that 1.587 x 10^3 g (or 1.587 kg) of wood would be required to heat the bathtub.

c) At last, we need to calculate the amount of wood required to heat the bathtub when it only has an efficiency of 30%.

Since we calculated the amount of wood needed considering 100% efficiency, we can use that number and consier now 30% efficiency:

100% efficiency ---------- 1.587 kg of wood

30% efficiency ----------- y

Note that now we have a different relation between the numbers (inversely proportional) and we calculate y as following:

Therefore, considering only 30% of efficiency, 5.290 kg of wood would be required to heat the tub.