Question

Solve your answers using inequalities using a number line strategy or a factor table strategy. Express your answers using set notation. (x+1)(x+3) ≥ 0

Answer 1

Given the inequality;

`(x+1)(x+3)\ge0`

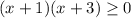
We can begin by finding the signs of the factors;

`\begin{gathered} \text{For (x+1);} \\ x+1=0\Rightarrow x=-1 \\ x+1<0\Rightarrow x<-1 \\ x+1>0\Rightarrow x>-1 \end{gathered}`
`\begin{gathered} \text{For (x+3);} \\ x+3=0\Rightarrow x=-3 \\ x+3>0\Rightarrow x>-3 \\ x+3<0\Rightarrow x<-3 \end{gathered}`

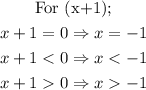
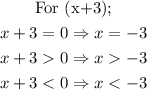
We can now identify the intervals that satisfy the required condition "greater than or equal to zero."

`\begin{gathered} x<-3\text{ OR x}=-3 \\ x=-1\text{ OR x}>-1 \end{gathered}`

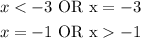
This on the number line would now look like;

ANSWER:

`\begin{gathered} x\le-3 \\ OR \\ x\ge-1 \end{gathered}`

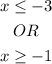
Expressing the number;

`x\le-3`

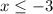
in set notation;

`\mleft\lbrace x\in Z\mright|x\le-3\}`

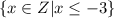
This means;

"x is a member of the set of integers such that x is less than or equla to negative 3."

The symbol that looks like an "E" means is a member of, the one that looks like a capital Z means set of integers, the slash means "such that...".

We would not use natural numbers because negatives do not occur naturally.