ANSWER:
46.1 miles/hr
Explanation:
We calculate the x and y coordinates of each vector just like this:
For the plane:
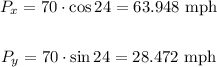
For the wind:
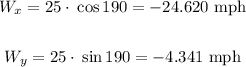
We calculate the resulting vector:
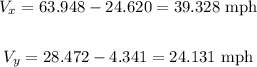
Now, we calculate the norm of the vector as follows:
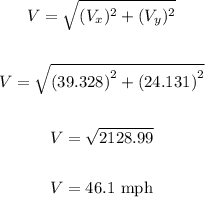
The speed of the plane is 46.1 miles per hour.