Question

Factored Form : g(t)=(t-1) (t+1) (t+2). Standard Form: . C. Graph g(t) . Be sure to show x-intercept(s) . and behaviors. D. If the stock continued to grow forever, what would the price approach? Be sure to use the end behavior notation.

Answer 1

Graph Below

`\begin{gathered} t\rightarrow+\infty,\text{ g(t) }\rightarrow+\infty, \\ t\rightarrow-\infty,\text{ g(t)}\rightarrow-\infty \end{gathered}`

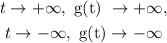
t³+2t²+t-y=2 The Standard form.

1) Let's plot that function. And then analyze the graph. We need to set a table

for t and g(t) values.

As we can see the x-intercepts are x=-2, and x=1. As the behavior we have:

As t goes infinitely positive values then g(t) or y goes the same way. When t goes infinitely negative values, y or g(t) goes the same way:

`\begin{gathered} t\rightarrow+\infty,\text{ g(t) }\rightarrow+\infty, \\ t\rightarrow-\infty,\text{ g(t)}\rightarrow-\infty \end{gathered}`

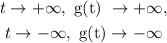
As we can see in this sketch:

The standard form is obtained from the distribution of the factors, and rewriting it as ax+by = c:

g(t)=(t-1) (t+1) (t+2)

g(t) =t³+2t²-t-2

y=t³+2t²-t-2

-t³-2t²-t+y =2

t³+2t²+t-y=2