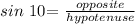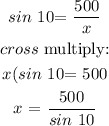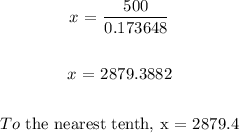Question

Find the value of x. Round the length to the nearest tenth. The diagram is not drawn to scale. (image attached)thank you ! :)

Answer 1

Answer:

x = 2879.4 m

Step-by-step explanation:

Given:

A right-angled triangle with one side and a known angle

To find:

the value of x

To determine x, we need to apply the alternate angles to get the angle in the triangle

Using an illustration:

angle = 10°

opposite = side opposite the angle = 500m

hypotenuse = x

To get x, we will apply sine ratio (SOH):

`sin\text{ 10\degree = }(opposite)/(hypotenuse)`

`\begin{gathered} sin\text{ 10\degree = }(500)/(x) \\ cross\text{ multiply:} \\ x(sin\text{ 10\degree\rparen = 500} \\ x\text{ = }\frac{500}{sin\text{ 10\degree}} \end{gathered}`

`\begin{gathered} x\text{ = }(500)/(0.173648) \\ \\ x\text{ = 2879.3882} \\ \\ To\text{ the nearest tenth, x = 2879.4} \end{gathered}`