We want to derive the quadratic formula from the following expression
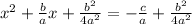
The next step would be rewrite the left side of the equation as the square of a sum, and combine the two terms on the right side of the equation on a single fraction.
Let's start by rewriting the left side.
When we expand the square of a binomial, we have
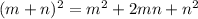
In our expression, we have
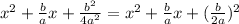
Comparing our expression with the expansion of a squared binomial, we have
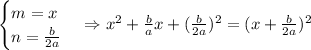
Then, our original expression can be rewritten as

And finally, by combining the terms on the right side, we have
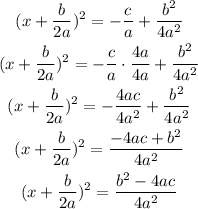
This is the next step. The answer is option C.